•Notícia

• Nota de premsa

Els matemàtics de la Universitat Politècnica de Catalunya (UPC) Enrique Bendito, Ángeles Carmona, Andrés M. Encinas i José Manuel Gesto han resolt un problema matemàtic clàssic, que té un segle d’antiguitat, conegut com el “problema dels punts de Fekete”. El grup ha desenvolupat un algorisme que té aplicacions a la biologia i la química. L'abast de la validesa d’aquesta eina s’ha provat gràcies a la potència de càlcul del superodinador FinisTerrae, i ara s’obren les portes per resoldre problemes matemàtics encara més complexos.

El “problema dels punts de Fekete” consisteix en “determinar la posició d’un cert nombre de punts sobre un objecte, de manera que l’energia potencial produïda per la interacció d’aquests punts sigui mínima”, segons Enrique Bendito. És a dir, si hi ha una sèrie de partícules que tenen influència unes sobre les altres, per exemple partícules amb carrega elèctrica, es tracta de distribuir-les sobre la superfície d’un objecte de manera que interfereixin el mínim possible, fent que les interaccions entre elles es compensin i arribin a un estat d’equilibri.

Trobar una configuració adient dels punts esdevé més complicat quan augmenten el número de partícules i la geometria de l’objecte on s’han de situar esdevé més irregular.

Aquest grup de recerca del Departament de Matemàtica Aplicada III ha desenvolupat un algorisme que dóna solucions per a una extensa gamma de geometries i per a diferents tipus de d’interacció entre les partícules.

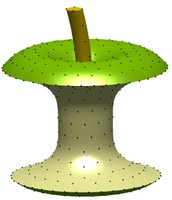
Aquest algorisme va molt més lluny que els que s’havien creat fins ara per resoldre el problema: no necessita tant de temps de càlcul per obtenir la configuració dels punts, no treballa únicament sobre esferes, si no que treballa amb objectes de geometries molt més complexes, com ara plàtans, pomes o poliedres. I a més, es capaç de situar sobre l’objecte molts més punts “en equilibri” que els treballs previs.

La validesa d’aquest algorisme ja s’havia demostrat amb ordinadors convencionals, tal com es va publicar l’any 2007 a la revista Journal of Computational Physics. Tanmateix, gràcies al supercomputador FinisTerrae, situat al Centre de Computació de Galicia (CESGA), han pogut provar la validesa de l’algorisme amb un número de punts molt més gran.

Fins ara, els algorismes que s’aproximaven al problema, havien aconseguit situar uns pocs milers de punts sobre una esfera. L’algorisme dels investigadors de la UPC, treballant amb el FinisTerrae, ha aconseguit trobar configuracions “en equilibri” sobre una esfera de fins a 50.000 punts. A més, per a posar a prova la capacitat de l’algorisme s’ha arribat a abordar el problema fins amb un milió de punts. “Amb el FinisTerrae hem constat clarament que el nostre algorisme és robust, versàtil i eficient”, explica José Manuel Gesto.

El CESGA va establir el repte de resoldre el problema de punts de Fekete amb l’ajuda del supercomputador per posar a prova la capacitat de càlcul del FinisTerrae durant el seu període de proves. La feina del superordinador, desenvolupada durant dos setmanes al mes de febrer, ha exigit unes 350.000 hores de càlcul. Si s’hagués utilitzat només una CPU del FinisTerrae, haurien calgut 40 anys per fer el càlcul. Quan es va fer el càlcul amb un milió de punts, 1.024 CPUs van treballar en paral.lel durant un dia i mig.

El grup de la UPC ha estat treballant durant cinc anys amb aquest algorisme, que es pot aplicar en “qualsevol recerca que treballi amb la interacció de partícules segons la mecànica clàssica”. La recerca bàsica que s’ha efectuat permet oferir una eina que serà útil en estudis biològics o químics. Per exemple, l’algorisme té aplicacions “en estudis de conformació de molècules i estructures cristal·lines, de gasos, virus, proteïnes o bactèries”, explica Bendito.

De fet, el comportament d’elements biològics està afectat per forces naturals (d’atracció, de repulsió, etc.) que es regeixen per les lleis de la mecànica. En aquest sentit, l’algorisme ajudarà a modelar el comportaments d’elements biològics.

La cerca dels punts de Fekete és un pas endavant per resoldre un altre problema clau de les matemàtiques modernes: el problema 7 de Smale. A finals del segle XX la Unió Matemàtica Internacional va preguntar quins serien els principals problemes que quedaven per resoldre al s.XXI, i el prestigiós matemàtic Stephen Smale va donar una llista de 18 problemes, el seté dels quals està molt lligat als punts de Fekete. El problema 7 planteja la possibilitat de trovar configuracions suficientment properes a les òptimes sobre una esfera en un temps polinòmic. Aquests configuracions servirien per resoldre determinats sistemes d’equacions. Gràcies al nou algorisme i el FinisTerrae s’han obtingut més de 50 milions de formes de disposar els punts sobre l’esfera, que és “la mostra més gran obtinguda fins ara sobre el problema 7 de Smale”, afirma Gesto.