•Noticia

Los matemáticos de la Universidad Politécnica de Cataluña (UPC) Enrique Bendito, Ángeles Carmona, Andrés M. Encinas y José Manuel Gesto han resuelto un problema matemático clásico, que tiene un siglo de antigüedad, conocido como el “problema de los puntos de Fekete". El grupo ha desarrollado un algoritmo que tiene aplicaciones en biología y química. El alcance de la validez de esta herramienta se ha probado gracias a la potencia de cálculo del superordenador FinisTerrae, y ahora se abren las puertas para resolver problemas matemáticos todavía más complejos.

El “problema de los puntos de Fekete” consiste en determinar "la posición de un cierto número de puntos sobre un objeto, de forma que la energía potencial producida por la interacción de dichos puntos sea mínima", según Enrique Bendito. Es decir, si existe una serie de partículas que tienen influencia unas sobre otras, por ejemplo partículas con carga eléctrica, se trata de distribuirlas sobre la superficie de un objeto de forma que interfieran el mínimo posible, de tal modo que las interacciones entre ellas se compensen y lleguen a un estado de equilibrio.

Hallar una configuración adecuada de los puntos es más complicado cuando aumenta el número de partículas y la geometría del objeto en el que tienen que situarse es más irregular.

Este grupo del Departamento de Matemática Aplicada III ha desarrollado un algoritmo que ofrece soluciones para una extensa gama de geometrías y para distintos tipos de interacción entre las partículas.

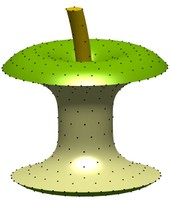
Este algoritmo va mucho más lejos que los algoritmos creados hasta ahora para resolver el problema: no necesita tanto tiempo de cálculo para obtener la configuración de los puntos y no trabaja únicamente sobre esferas, sino que trabaja con objetos de geometrías mucho más complejas, como plátanos, manzanas o poliedros. Además, es capaz de situar sobre el objeto muchos más puntos “en equilibrio" que los trabajos previos.

La validez de este algoritmo ya se había demostrado con ordenadores convencionales, como se publicó en el año 2007 en la revista Journal of Computational Physics. Sin embargo, gracias al superordenador FinisTerrae, situado en el Centro de Computación de Galicia (CESGA), se ha podido probar la validez del algoritmo con un número de puntos mucho mayor.

Hasta ahora, los algoritmos que se aproximaban al problema habían conseguido situar unos pocos millares de puntos sobre una esfera. El algoritmo de los investigadores de la UPC, trabajando con el FinisTerrae, ha conseguido alcanzar configuraciones “en equilibrio" sobre una esfera de hasta 50.000 puntos. Además, para poner a prueba la capacidad del algoritmo se ha llegado a abordar el problema hasta con un millón de puntos. ”Con el FinisTerrae hemos constatado claramente que nuestro algoritmo es robusto, versátil y eficiente", explica José Manuel Gesto.

El CESGA acometió el reto de resolver el problema de puntos de Fekete con la ayuda del superordenador para poner a prueba la capacidad de cálculo del FinisTerrae durante su periodo de pruebas. El trabajo del superordenador, desarrollado durante dos semanas del mes de febrero, exigió unas 350.000 horas de cálculo. Si se hubiera utilizado sólo una CPU del FinisTerrae, habrían hecho falta 40 años para realizar el mismo cálculo. Cuando el cálculo se efectuó con un millón de puntos, 1.024 CPU trabajaron en paralelo durante un día y medio.

El grupo de la UPC ha estado trabajando durante cinco años con este algoritmo, que se puede aplicar a cualquier investigación que trabaje con la interacción de partículas según la mecánica clásica. La investigación básica que se ha efectuado permite ofrecer una herramienta que será útil en estudios biológicos y químicos. Por ejemplo, el algoritmo tiene aplicaciones “en estudios de conformación de moléculas y estructuras cristalinas, de gases, virus, proteínas o bacterias," explica Bendito. De hecho, el comportamiento de elementos biológicos se ve afectado por fuerzas naturales (de atracción, de repulsión, etc.) que se rigen por las leyes de la mecánica. En este sentido, el algoritmo ayudará a modelizar el comportamiento de elementos biológicos.

La investigación sobre los puntos de Fekete es un paso más para resolver otro problema clave de las matemáticas modernas: el problema 7 de Smale. A finales del siglo XX, la Unión Matemática Internacional preguntó cuáles serían los principales problemas que quedarían por resolver en el siglo XXI, pregunta a la que el prestigioso matemático Stephen Smale respondió dando una lista de 18 problemas, el séptimo de los cuales tiene mucho que ver con los puntos de Fekete. Plantea la posibilidad de hallar configuraciones suficientemente próximas a las óptimas sobre una esfera en un tiempo polinómico. Estas configuraciones servirían para resolver determinados sistemas de ecuaciones. Gracias al nuevo algoritmo y al FinisTerrae se han obtenido más de 50 millones de formas de disponer los puntos sobre la esfera, que es ”la mayor muestra obtenida hasta ahora sobre el problema 7 de Smale", afirma Gesto.